Answer:
The area of the shaded region is 11.606 square centimeters.
Explanation:
The area of the shaded region is obtained by subtracting the area of the triangle from the area of the circular section. The area of the triangle (
 ), in square centimeters, can be calculated by the Heron's formula:
), in square centimeters, can be calculated by the Heron's formula:
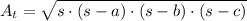 (1)
(1)
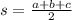 (2)
(2)
Where:
 ,
,
 ,
,
 - Lengths of the sides of the triangle, in centimeters.
- Lengths of the sides of the triangle, in centimeters.
 - Semiperimeter, in centimeters.
- Semiperimeter, in centimeters.
If we know that
 and
and
 , then the area of the triangle is:
, then the area of the triangle is:
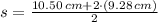
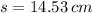

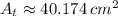
And the area of the circular section (
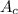 ), in square centimeters, is determined by the following formula:
), in square centimeters, is determined by the following formula:
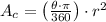 (3)
(3)
Where:
 - Radius of the circle, in centimeters.
- Radius of the circle, in centimeters.
 - Internal angle, in sexagesimal degrees.
- Internal angle, in sexagesimal degrees.
If we know that
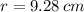 and
and
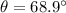 , then the area of the circular section is:
, then the area of the circular section is:
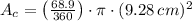
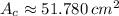
Finally, the area of the shaded region (
 ), in square centimeters, is:
), in square centimeters, is:
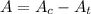 (4)
(4)

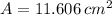
The area of the shaded region is 11.606 square centimeters.