Question

Factorise the expression:
x^2 - 144

and

2ax – 6ay + bx – 3by

Answer 1

(x-12)(x+12) and (2a+b)(x-3y)

Explanation:

So first we have:

x^2-144

The key here is that there is no bx in the ax^2+bx+c equation here.

This means that b must equal 0, or in other words, cancel itself out.

To do this, first, the two factors must have opposite signs, and secondly, the blank values must be equal (x+_) * (x-_)

What could they be? The c value, 144, equals the two blank values multiplied together. Since they are in the same in this case, blank value^2 = 144, or
`√(144) = blank`

`√(144) = 12`

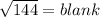
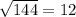
So the answer is:

(x+12)(x-12)

Next we have:

2ax - 6ay + bx - 3by

This is a bit more tricky, but first we must facor out some numbers/variables to simplify.

Lets seperate the two parts of this equation:

2ax - 6ay and bx - 3by

Now lets look at:

2ax - 6ay

How can we simplify this? Factor the 2a, which both have in common:

2a(x-3y)

Now lets look at and factor it too:

bx - 3by

Only b can be factored out, which gives us:

b(x-3y)

Now lets put this back into our orginal equation:

2a(x-3y) + b(x-3y)

Both of these have x-3y. Concidence? Nope!

From the way we split the equation into two pieces and factored, the two x-3ys are actually the same, and we can combine them!

Then, the 2a and the +b can be combined to give us:

(2a+b)

Puttting these together gives us:

(2a+b)(x-3y)

Hope this helps!