Question

Please help ASAP!!! THANKS!

Answer 1

Given:

The vertices of a parallelogram GHJK are K(1,2), J(5,2), G(0,8).

To find:

The coordinate of the vertex H.

Solution:

We know that the diagonals of a parallelogram bisects each other. It means the midpoint of the diagonals are same.

Let the coordinate of the vertex H are (a,b).

Midpoint formula:

`Midpoint=\left((x_1+x_2)/(2),(y_1+y_2)/(2)\right)`

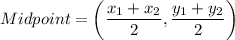
In parallelogram GHJK ,

Midpoint of diagonal GJ = Midpoint of diagonal HK

`\left((0+5)/(2),(8+2)/(2)\right)=\left((a+1)/(2),(b+2)/(2)\right)`

`\left((5)/(2),(10)/(2)\right)=\left((a+1)/(2),(b+2)/(2)\right)`

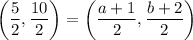
On comparing both sides, we get

`(5)/(2)=(a+1)/(2)`

`5=a+1`

`5-1=a`

`4=a`

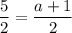
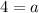
And,

`(10)/(2)=(b+2)/(2)`

`10=b+2`

`10-2=b`

`8=b`

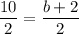
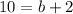
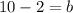
Therefore, the coordinates of the vertex H are (4,8). Hence, option B is correct.