Question

Find lim h->0 f(9+h)-f(9)/h if f(x)=x^4 a. 23 b. -2916 c. 2916 d. 2925

Answer 1

`\displaystyle\lim_(h\to0)\frac{f(9+h)-f(9)}h = \lim_(h\to0)\frac{(9+h)^4-9^4}h`

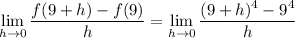
Carry out the binomial expansion in the numerator:

`(9+h)^4 = 9^4+4*9^3h+6*9^2h^2+4*9h^3+h^4`

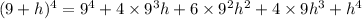
Then the 9⁴ terms cancel each other, so in the limit we have

`\displaystyle \lim_(h\to0)\frac{4*9^3h+6*9^2h^2+4*9h^3+h^4}h`

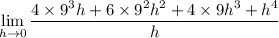
Since h is approaching 0, that means h ≠ 0, so we can cancel the common factor of h in both numerator and denominator:

`\displaystyle \lim_(h\to0)(4*9^3+6*9^2h+4*9h^2+h^3)`

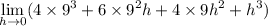
Then when h converges to 0, each remaining term containing h goes to 0, leaving you with

`\displaystyle\lim_(h\to0)\frac{f(9+h)-f(9)}h = 4*9^3 = \boxed{2916}`

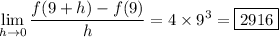
or choice C.

Alternatively, you can recognize the given limit as the derivative of f(x) at x = 9:

`f'(x) = \displaystyle\lim_(h\to0)\frac{f(x+h)-f(x)}h \implies f'(9) = \lim_(h\to0)\frac{f(9+h)-f(9)}h`

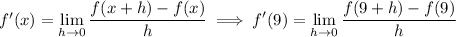
We have f(x) = x ⁴, so f '(x) = 4x ³, and evaluating this at x = 9 gives the same result, 2916.