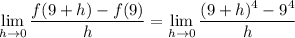
Carry out the binomial expansion in the numerator:
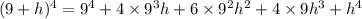
Then the 9⁴ terms cancel each other, so in the limit we have
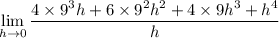
Since h is approaching 0, that means h ≠ 0, so we can cancel the common factor of h in both numerator and denominator:
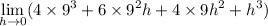
Then when h converges to 0, each remaining term containing h goes to 0, leaving you with
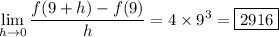
or choice C.
Alternatively, you can recognize the given limit as the derivative of f(x) at x = 9:
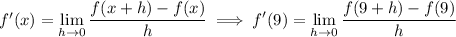
We have f(x) = x ⁴, so f '(x) = 4x ³, and evaluating this at x = 9 gives the same result, 2916.