Question

In a circle of radius 10 cm, a sector has an area of 40 (pi) sq. cm. What is the degree measure of the arc of the sector?

72
144
180°

Answer 1

Solution :-

We know that

Area = πr²

Area = 3.14 × (10)²

Area = 314/100 × 100

Area = 314 cm²

Now

40π/314 = x/360

40 × 3.14/314 = x/360

125.6/314 = x/360

0.4 = x/360

0.4 × 360 = x

144 = x

`\\`

Answer 2

144°

Explanation:

First, find the area of the circle, with the formula A =
`\pi`r²

Plug in 10 as the radius, and solve

A =
`\pi`r²

A =
`\pi`(10²)

A = 100
`\pi`

Using this, create a proportion that relates the area of the sector to the degree measure of the arc.

Let x represent the degree measure of the arc of the sector:

`(40\pi )/(100\pi )` =
`(x)/(360)`

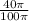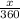
Cross multiply and solve for x:

100
`\pi`x = 14400
`\pi`

x = 144

So, the degree measure of the sector arc is 144°