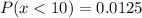Answer:
"0.0125" is the right solution.
Explanation:
The given values are:
Random sample,
n = 90
Claims,
p = 20%
or,
= 0.20
By using normal approximation, we get
⇒
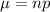
On substituting the values, we get
⇒
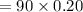
⇒
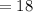
Now,
The standard deviation will be:
⇒
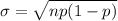
On putting the above given values, we get
⇒
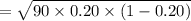
⇒
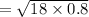
⇒
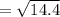
⇒
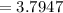
hence,
By using the continuity correction or the z-table, we get
⇒
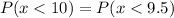
⇒
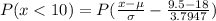
⇒
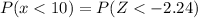
From table,
⇒