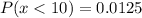Question

A politician claims that 20% of the millions of votes cast for his opponent are fraudulent. To test this claim, an investigator collects a random sample of 90 ballots and contacts the voters whose names appear on the ballots to determine if each ballot is in fact fraudulent. Use a normal approximation to find the probability that less than 10 of the selected ballots turn out to be fraudulent, assuming the politician's claim is correct.

Answer 1

"0.0125" is the right solution.

Explanation:

The given values are:

Random sample,

n = 90

Claims,

p = 20%

or,

= 0.20

By using normal approximation, we get

⇒
`\mu = np`

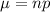
On substituting the values, we get

⇒
`=90* 0.20`

⇒
`=18`

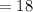
Now,

The standard deviation will be:

⇒
`\sigma=√(np(1-p))`

On putting the above given values, we get

⇒
`=√(90* 0.20* (1-0.20))`

⇒
`=√(18* 0.8)`

⇒
`=√(14.4)`

⇒
`=3.7947`

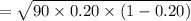
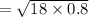
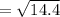
hence,

By using the continuity correction or the z-table, we get

⇒
`P(x < 10) = P(x < 9.5)`

⇒
`P(x < 10) = P((x-\mu)/(\sigma) -(9.5-18)/(3.7947) )`

⇒
`P(x < 10) = P(Z < -2.24)`

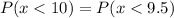
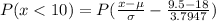
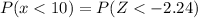
From table,

⇒
`P(x < 10) = 0.0125`