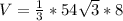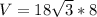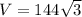Question

Blank 1: The Base Area (B) of the pyramid is _ cm2. --> Area = (1/2)ap

Blank 2: The height (h) of the pyramid is _ cm.


Blank 3: The Volume (V) of the pyramid is _ cm3.


Use the formula V = (1/3)Bh to find the volume of the hexagonal pyramid.

Answer 1

See Explanation

Explanation:

The question is incomplete, as the dimensions of the hexagon are not given.

I will assume that:

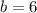`b = 6` --- base length

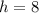`h = 8` --- height

First, we calculate the height (a) of each triangle that makes the hexagonal base

The formula to use is:

`a^2 = b^2 - ((b)/(2))^2`

`a^2 = 6^2 - ((6)/(2))^2`

`a^2 = 6^2 - (3)^2`

`a^2 = 36 - 9`

`a^2 = 27`

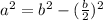
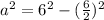
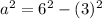
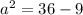
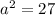
Take positive square roots

`a = \sqrt{27`

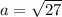
Expand

`a = \sqrt{9*3`

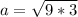
Split

`a = √(9)*\sqrt3`

`a = 3\sqrt3`

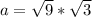
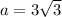
So, we have:

`Area = (1)/(2)ap`

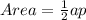
Where

`a = 3\sqrt3`

`p =perimeter`

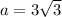
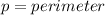
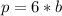`p = 6 * b` ---- 6 represents the sides of the hexagon

`p = 6 * 6`

`p = 36`

`B= (1)/(2)ap`

`B= (1)/(2) * 3\sqrt 3 * 36`

`B= 3\sqrt 3 *18`

`B = 54\sqrt 3`

`h = 8`

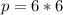
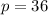
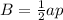
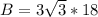
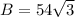
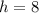
Lastly, the volume is:

`V = (1)/(3)Bh`

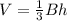
So:

`V = (1)/(3) * 54\sqrt3 * 8`

`V = 18\sqrt3 * 8`

`V = 144\sqrt3`