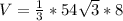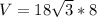Answer:
See Explanation
Explanation:
The question is incomplete, as the dimensions of the hexagon are not given.
I will assume that:
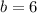 --- base length
--- base length
 --- height
--- height
First, we calculate the height (a) of each triangle that makes the hexagonal base
The formula to use is:


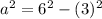
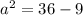
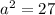
Take positive square roots
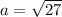
Expand
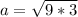
Split
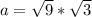
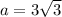
So, we have:
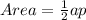
Where
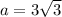
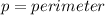
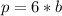 ---- 6 represents the sides of the hexagon
---- 6 represents the sides of the hexagon
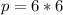
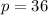
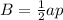

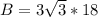


Lastly, the volume is:
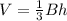
So: