Question

A spring is hung from the ceiling. When a block is attached to its end, it stretches 2.6 cm before reaching its new equilibrium length. The block is then pulled down slightly and released. What is the frequency of oscillation?

Answer 1

f = 3.09 Hz

Step-by-step explanation:

This is a simple harmonic motion exercise where the angular velocity is

w² =
`(k)/(m)`

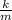
to find the constant (k) of the spring, we use Hooke's law with the initial data

F = - kx

where the force is the weight of the body that is hanging

F = W = m g

we substitute

m g = - k x

k =
`- (m g)/(x)`

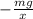
we calculate

k =
`- (9.8 m)/(- 2.6 \ 10^(-2))`

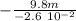
k = 3.769 10² m

we substitute in the first equation

w² =
`( 3.769 \ 10^2 \ m )/(m)`

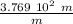
w = 19.415 rad / s

angular velocity and frequency are related

w = 2πf

f =
`(w)/(2\pi )`

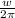
f = 19.415 / 2pi

f = 3.09 Hz