Answer:
Ratio of the volumes of the spheres and cube = 0.523
Explanation:
From the figure attached,
Diameter of one sphere = Half of the measure of one side of the cube
=
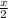
Radius of the sphere =
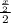
=
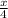
Volume of a cube is given by the formula,
V =
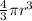
Therefore, volume of one sphere =
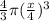
=
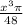
Volume of 8 spheres =
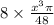
=

Volume of a cube = (side)³
=
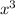
Ratio of the volumes of the sphere and cube =

=

≈ 0.523