Answer:
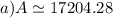
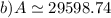

Explanation:
The amount formula in compound interest is:

where:
P = principal amount
r = annual interest
n = number of compounding periods
t = number of years
We already know that:
P = $10000
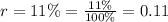
n = 4 (quarterly in a year)
a ) t = 5 years
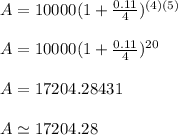
b) t = 10 years

c) t = 15 years
