Answer:
The p-value of the test is 0.0014 < 0.01, meaning that the data indicates that the true average unrestrained compressive strength is less than the design value of 3200.
Explanation:
We want to determine whether the data indicate that the true average unrestrained compressive strength is less than the design value of 3200.
At the null hypothesis, we test if the mean is at the design value of 3200, so:
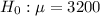
At the alternate hypothesis, we test if it is less than the design value of 3200, so:
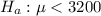
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis, s is the standard deviation of the sample and n is the size of the sample.
is the value tested at the null hypothesis, s is the standard deviation of the sample and n is the size of the sample.
3200 is tested at the null hypothesis:
This means that
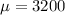
The sample average unrestrained compressive strength for 50 specimens of a particular type of brick was computed to be 3120 psi, and the sample standard deviation was 180.
This means that
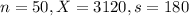
Test statistic:

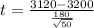
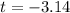
P-value of the test and decision:
The p-value of the test is the probability of finding a sample mean below 3120, which is the p-value of t = -3.14, using a one-tailed test, with 50 - 1 = 49 degrees of freedom.
With the help of a calculator, the p-value of the test is 0.0014
The p-value of the test is 0.0014 < 0.01, meaning that the data indicates that the true average unrestrained compressive strength is less than the design value of 3200.