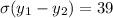Answer:
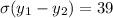
Explanation:
From the question we are told that:
Urn 1 :2 Red, 3 Yellow
Urn 2:3 Red, 7 Yellow
Sample 1
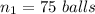
Sample 2
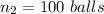
Generally the Probability of Red ball drawn is mathematically given by
For Urn 1
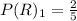
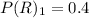
For Urn 2
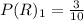
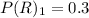
Generally the equation for Variance of two independent variables
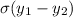 is mathematically given by
is mathematically given by
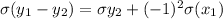
Where red balls drawn from both Urn is Modeled
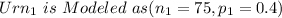
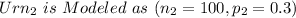
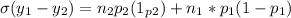
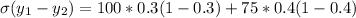
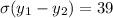
Therefore the variance of the random variable defined as the number of red balls is