Question

An architect wants to draw a rectangle with a diagonal of 13 centimeters. The length of the rectangle is to be 3 centimeters more than triple the width. What dimensions should she make the rectangle?​

Answer 1

The rectangle is 3.2 cm by 12.6 cm

Explanation:

See attached image for a diagram.

Choose w to represent the width because the length is described by referring to the width: it's 3 more than (add 3) triple (multiplied by 3) the width.

Length = 3w + 3

The diagonal forms two right triangles, each with leg = w, other leg = 3w + 3, hypotenuse = 13.

The Pythagorean Theorem says
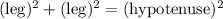`(\text{leg})^2+(\text{leg})^2=(\text{hypotenuse})^2` so

`w^2+(3w+3)^2=13^2\\\\w^2+9w^2+18w+9=169\\\\10w^2+18w-160=0\\\\5w^2+9w-80=0\\`

Now solve using the Quadratic Formula with
`a=5,\,b=9,\,c=-80`.

`w=(-b\pm√(b^2-4ac))/(2a)\\w=(-9\pm√(81+1600))/(10)\\\\w=(-9\pm√(1681))/(10)\\\\w=(-9\pm41)/(10)\\\\w=-5\text{ or }w=3.2`

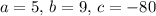The negative root makes no sense as a distance, so the width of the rectangle is 3.2 cm. The length is 3(3.2) + 3 = 12.6 cm.