Solution :
Mean time for an automobile to run a 5000 mile check and service = 1.4 hours
Standard deviation = 0.7 hours
Maximum average service time = 1.6 hours for one automobile
The z - score for 1.6 hours =
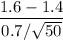
= 2.02
Now checking a normal curve table the percentage of z score over 2.02 is 0.0217
Therefore the overtime that will have to be worked on only 0.217 or 2.017% of all days.