Question

The company PureNSafe is designing a portable, solar-powered disinfection system for Army use only. The system is simply an inlet pipe, a pump, a mixing chamber and an outlet pipe. The water is continuously pumped into the chamber where it is irradiated with UV light before it exits through the the appropriate tube into a collection vessel. The disinfection rate constant rate of disinfection with UV light is 7.80 s.1 and the amount of bacteria has to be reduced by 99.9%. be reduced by 99.9%. Since the Army requires an object that can be carried in a backpack, it requires that the chamber of the apparatus must not hold a capacity greater than 2 L. How much water will the system be able to produce during 10 hours of sunshine?

Answer 1

The treatment system will operate as the well mixed chamber.

Disinfection rate constant for the UV light, k is 7.80 /s. Number of bacteria in water need to be reduced by 99.9%

Percent reduction of bacteria should be
`$(1-10^(0.99)) * 100 =89.7\%$`

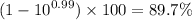
Volume of the unit chamber is fixed at 2L

Assume the inlet concentration,
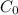`$C_0$` as 1000

The outlet concentration of bacteria, C should be
`$1000-\left(1000 * (89.7)/(100)\right)$`

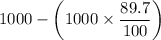
= 103

The well mixed chamber will then follow a completely mixed flow reactor model.

Compute the time required :

`$t=(1)/(k)\left((C_0)/(C)-1\right)$`

`$t=(1)/(7.8)\left((1000)/(103)-1\right)$`

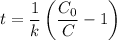
= 1.115 s

Flow through the system is
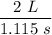`$(2 \ L)/(1.115 \ s)$` = 1.79 L/s

The amount of water treated during the 10 hours of sunlight is 1.79 x 10 x 60 x 60 = 64440 L