Answer:
Function 2 has larger max value.
Explanation:
We know that the graph of Function 1 has the maximum value of 1 at x = 4 by looking at the graph.
But since we don't know what the maximum value of Function 2 is (Because Function 2 isn't given as a graph but rather an equation.) which means that we have to find the maximum value of Function 2.
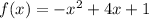
It is not necessary to find x-value for a function because we want to know which function has larger maximum value. We will be using the formula below.
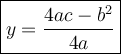
As you may know, a max-min value is indeed y-value. From Function 2, we know the value of a, b and c from standard form y = ax²+bx+c
Substitute our a, b and c in the formula.
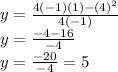
Since our maximum value or y-value is 5 for Function 2. Since we also know that Function 1 has 1 as maximum value and Function 2 has 5 as maximum value. Therefore, Function 2 has larger maximum value.