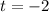Answer:
The test statistic for Norah's test is
Explanation:
Norah is in charge of a quality control test that involves measuring the amounts in a sample of bottles to see if the sample mean amount is significantly different than 500 ml.
This means that at the null hypothesis we test if the sample mean is 500 ml, that is:
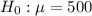
At the alternate hypothesis, we test if it is differente than 500 ml, that is:
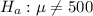
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis, s is the standard deviation of the sample and n is the size of the sample.
is the value tested at the null hypothesis, s is the standard deviation of the sample and n is the size of the sample.
500 is tested at the null hypothesis:
This means that

She takes a random sample of 16 bottles and finds a mean amount of 497ml, and a sample standard deviation of 6ml.
This means that
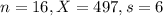
Calculate the test statistic for Norah's test.

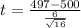
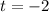
The test statistic for Norah's test is