Question

DE is parallel to AC. Find the lengths of AC and AD. FAST!!!

Answer 1

AC = 12.5, AD = 3

Explanation:

A line parallel to a side of a triangle and intersecting the other 2 sides, divides those sides proportionally, that is

`(BD)/(BE)` =
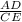`(AD)/(CE)` , substitute values

`(2)/(4)` =
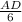`(AD)/(6)` ( cross- multiply )

4 AD = 12 ( divide both sides by 4 )

AD = 3

-----------------------------------------

Δ BDE and Δ BAC are similar, so the ratios of corresponding sides are equal, that is

`(DE)/(AC)` =
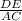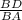`(BD)/(BA)` , substitute values

`(5)/(AC)` =
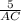`(2)/(5)` ( cross- multiply )

2 AC = 25 ( divide oth sides by 2 )

AC = 12.5

Answer 2

we have:

∆BDE is similar to ∆BAC

so their side are proportional :

BD/BD=BE/BC

2/BD=4/(6+4)

BD=2×10/4

BD=5

again

BE/BC=DE/AC

4/10=5/AC

AC=5×10/4

AC=25/2

Now,

AC=25/2 or 12.5.

AD=BA-BD=5-2=3.

is your answer.