Question

A mother is now 2 and ahalf times old as her daughter Mary. Four years ago the ratio of their ages was 3:1. Find the present age of the mother.

Answer 1

Given:

A mother is now 2 and a half times old as her daughter Mary.

Four years ago the ratio of their ages was 3:1.

To find:

The present age of the mother.

Solution:

Let x be the present age Mary's mother and y be the present age of Mary.

A mother is now 2 and a half times old as her daughter Mary. So,

`x=2(1)/(2)y`

`(x)/(y)=(2(2)+1)/(2)`

`(x)/(y)=(5)/(2)`

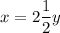
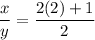
It means the ratio of their present age is 5:2. Let 5z be the present age of Mary's mother and 2z be the present age of Mary.

Four years ago the ratio of their ages was 3:1.

`(5z-4)/(2z-4)=(3)/(1)`

`1(5z-4)=3(2z-4)`

`5z-4=6z-12`

`-4+12=6z-5z`

`8=z`

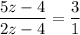
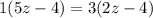
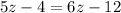
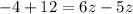
Now, the present age of the mother is:

`5z=5(8)`

`5z=40`

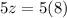
Therefore, the present age of the mother is 40 years.