Question

Find the area of the trapezoid below to the nearest tenth.

Answer 1

Area of trapezoid = 67.6 square units

Explanation:

Area of a trapezoid is given by the expression,

Area of the trapezoid =
`(1)/(2)(b_1+b_2)h`

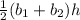
Here,
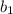`b_1` and
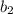`b_2` are the parallel sides of the given trapezoid.

And '
`h`' = Height between the parallel sides

From the given triangle ABE,

m(∠ABE) = m(∠ABC) - m(∠EBC)

m(∠ABE) = 120° - 90°

= 30°

By applying cosine rule in the given triangle,

cos(30°) =
`\frac{\text{Adjacent side}}{\text{Hypotenuse}}`

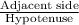
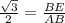
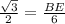
`(√(3) )/(2)=(BE)/(AB)`

`(√(3) )/(2)=(BE)/(6)`

BE =
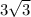`3√(3)` units

By applying sine rule in ΔABE,

sin(30°) =
`\frac{\text{Opposite side}}{\text{Hypotenuse}}`

`(1)/(2)=(AE)/(AB)`

`(1)/(2)=(AE)/(6)`

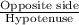
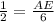
AE = 3 units

Length of
`b_1=BC=10`

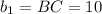
Length of
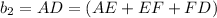`b_2=AD=(AE+EF+FD)` [AE = FD, since given trapezoid ABCD is an isosceles trapezoid]

`b_2=3+10+3`

`b_2=16`

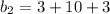
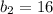
Height between the parallel sides
`h=3√(3)`

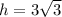
Area of the trapezoid =
`(1)/(2)(BC+AD)BE`

=
`(1)/(2)(10+16)(3√(3))`

=
`39√(3)`

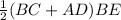
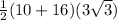
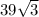
= 67.6 square units