Answer:
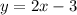
Explanation:
Hi there!
Slope-intercept form:
 where m is the slope and b is the y-intercept (the value of y when the line crosses the y-axis)
where m is the slope and b is the y-intercept (the value of y when the line crosses the y-axis)
1) Determine the slope (m)
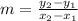 where the two given points are
where the two given points are
 and
and

Plug in the given points (2,1) and (4,5)
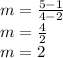
Therefore, the slope of the line is 2. Plug this into
 :
:
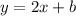
2) Determine the y-intercept (b)
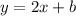
Plug in one of the given points and isolate b
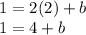
Subtract both sides by 4
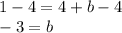
Therefore, the y-intercept of the line is -3. Plug this into
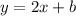 :
:
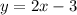
I hope this helps!