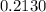Answer:
The probability is
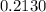
Step-by-step explanation:
Let's start by defining our variable :
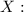 '' Number of students completing a degree in four year college enrolled in a two year college in the previous 10 years ''
'' Number of students completing a degree in four year college enrolled in a two year college in the previous 10 years ''
Now, let's suppose that we have an experiment compounded by a series of test. Each test result can be classified as '' success '' or '' failure ''. In each test, the success probability is called ''p'' and the failure probability is '' 1 - p ''. Both probabilities don't change from test to test and we also suppose that exists independence between each test. Therefore, the random variable
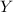 : '' Number of successes in n tests '' can be modeled as a binomial random variable. We write :
: '' Number of successes in n tests '' can be modeled as a binomial random variable. We write :
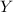 ~ Bi ( n , p )
~ Bi ( n , p )
Where ''n'' is the number of tests and ''p'' is the success probability.
In our question,
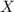 ~ Bi ( n , p ) ⇒
~ Bi ( n , p ) ⇒
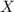 ~ Bi ( 10 , 0.49 )
~ Bi ( 10 , 0.49 )
We can think that asking to each of the graduate is our test and whose success probability is p = 0.49
The probability function for
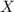 is :
is :
 ;
;
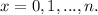
Where
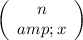 is the combinatorial number defined as
is the combinatorial number defined as
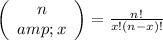
For this question, the probability function is :
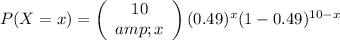 ;
;
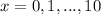
We need to calculate
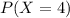 ⇒
⇒
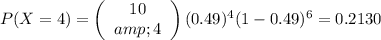
The probability is