Question

Suppose that a recent poll found that 47​% of adults believe that the overall state of moral values is poor. For 350 randomly selected​ adults, compute the mean and standard deviation of the random variable​ X, the number of adults who believe that the overall state of moral values is poor. What is the mean of X and the standard deviation of X?

Answer 1

The mean of X is 164.5 and the standard deviation is 9.34.

Explanation:

For each adult, there are only two possible outcomes. Either they believe that the overall state of moral values is poor, or they do not. The probability of an adult believing this is independent of any other adult, which means that the binomial probability distribution is used to solve this question.

Binomial probability distribution

Probability of exactly x sucesses on n repeated trials, with p probability.

The expected value of the binomial distribution is:

`E(X) = np`

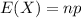
The standard deviation of the binomial distribution is:

`√(V(X)) = √(np(1-p))`

Suppose that a recent poll found that 47​% of adults believe that the overall state of moral values is poor.

This means that
`p = 0.47`

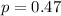
350 randomly selected​ adults

This means that
`n = 350`

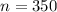
What is the mean of X and the standard deviation of X?

Mean:

`E(X) = np = 350*0.47 = 164.5`

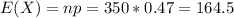
Standard deviation:

`√(V(X)) = √(np(1-p)) = √(350*0.47*0.53) = 9.34`

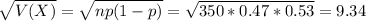
The mean of X is 164.5 and the standard deviation is 9.34.