Question

Hey i know this question is linked to Pythagorean theorem but i am still confused. So, please help me if you can ❤️

Answer 1

a = -10, b = 18

Explanation:

The Pythagorean Theorem is, indeed, involved. Use it to find an expression (you won't get a number!) for the height of the rectangle.

Using the right triangle, one leg has length x and hypotenuse length 8. for a moment, label the height h. Then

`x^2+h^2=8^3\\\\h^2=64-x^2\\\\h=√(64-x^2)`

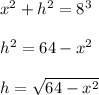
This expression tells the height of the rectangle, so it is the length of the two vertical sides. The top and bottom sides each have length x.

Perimeter = 20 says that the total length of all the sides is 20. Set that up and do a heap of algebra!

`x+x+√(64-x^2)+√(64-x^2)=20\\\\2x+2√(64-x^2)=20`

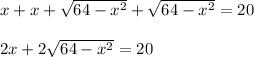
Divide by 2 (to simplify a bit).

`x +√(64-x^2)=10`

Subtract x to get the square root by itself (you'll see why in the next step).

`√(64-x^2)=10-x`

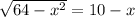
Square both sides of the equation.

`(√(64-x^2))^2=(10-x)^2\\\\\\64-x^2=100-20x+x^2\\\\64=100-20x+2x^2\\\\0=36-20x+2x^2`

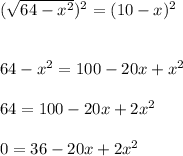
Divide by 2 again (because you can)

`0=18-10x+x^2`

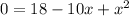
Rearrange terms to match the order in the question.

`x^2-10x+18=0`

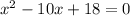
The coefficient of x is a = -10. The constant is b = 18.

Answer 2

Explanation:

From Pythagorean theorem, one of the sides can be determined as x^2 + y^2 =8^2

or y = (8^2 - x^2)^(1/2)

we can write the perimeter P as

P = 2x + 2y ---> 20 = 2x + 2(8^2 - x^2)^(1/2)

Dividing by 2, we get

10 = x + (8^2 - x^2)^(1/2)

Move the x to the other side,

10 - x = (8^2 - x^2)^(1/2)

Take the square of both sides to get rid of the radical sign:

(10 - x)^2 = 8^2 - x^2

Move everything to the left and expand the quantity inside the parenthesis:

x^2 + (100 - 20x + x^2) - 64 = 0

2x^2 - 20x + 64 = 0

or

x^2 - 10x + 32 = 0

Now we can see that a = -10 and b = 32