Answer:
a = -10, b = 18
Explanation:
The Pythagorean Theorem is, indeed, involved. Use it to find an expression (you won't get a number!) for the height of the rectangle.
Using the right triangle, one leg has length x and hypotenuse length 8. for a moment, label the height h. Then
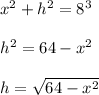
This expression tells the height of the rectangle, so it is the length of the two vertical sides. The top and bottom sides each have length x.
Perimeter = 20 says that the total length of all the sides is 20. Set that up and do a heap of algebra!
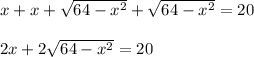
Divide by 2 (to simplify a bit).

Subtract x to get the square root by itself (you'll see why in the next step).
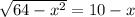
Square both sides of the equation.
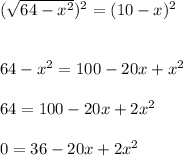
Divide by 2 again (because you can)
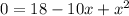
Rearrange terms to match the order in the question.
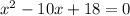
The coefficient of x is a = -10. The constant is b = 18.