Answer:
A. m<C = 57 degrees, a = 12, b = 19
Explanation:
First we can start by calculating Angle C by using the rule that all interior angles of a triangle always add to 180 degrees:
180 - (39+84) = C
180 - 123 = C
C = 57
Now let's calculate side a. We can do this by using the sin rule:
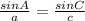
According to the diagram we know that Angle A is 39 degrees, Angle C is 57 degrees, and side c is 16 so we can substitute these values into the formula and solve:

We can use the same method to solve for side b:

We now have the following values:
Angle C = 57 degrees, a = 12, b = 19
We can now see that A/Number 1 is the correct option.
Hope this helped!