Answer:
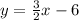
Explanation:
Hi there!
What we need to know:
- Linear equations are typically organized in slope-intercept form:
 where m is the slope of the line and b is the y-intercept (the value of y when the line crosses the y-axis)
where m is the slope of the line and b is the y-intercept (the value of y when the line crosses the y-axis)
- Parallel lines will always have the same slope but different y-intercepts.
1) Determine the slope of the parallel line
Organize 3x = 2y into slope-intercept form. Why? So we can easily identify the slope, m.
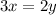
Switch the sides
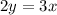
Divide both sides by 2 to isolate y
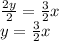
Now that this equation is in slope-intercept form, we can easily identify that
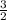 is in the place of m. Therefore, because parallel lines have the same slope, the parallel line we're solving for now will also have the slope
is in the place of m. Therefore, because parallel lines have the same slope, the parallel line we're solving for now will also have the slope
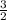 . Plug this into
. Plug this into
 :
:
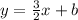
2) Determine the y-intercept
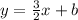
Plug in the given point, (4,0)
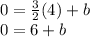
Subtract both sides by 6
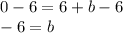
Therefore, -6 is the y-intercept of the line. Plug this into
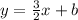 as b:
as b:
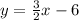
I hope this helps!