Question

Find x such that the line through (6, −3) and (7, 6) is perpendicular to the line through (−2, 5) and (x, −1).

Answer 1

Given:

The line through (6, −3) and (7, 6) is perpendicular to the line through (−2, 5) and (x, −1).

To find:

The value of x.

Solution:

Slope formula: If a line passes through two points, then the slope of the line is:

`m=(y_2-y_1)/(x_2-x_1)`

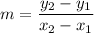
The slope of the line through (6, −3) and (7, 6) is:

`m_1=(6-(-3))/(7-6)`

`m_1=(6+3)/(1)`

`m_1=9`

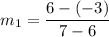
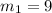
The slope of the line through (−2, 5) and (x, −1) is:

`m_2=(-1-5)/(x-(-2))`

`m_2=(-6)/(x+2)`

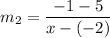
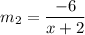
We know that the product of slopes of two perpendicular lines is -1.

`m_1\cdot m_2=-1`

`9\cdot (-6)/(x+2)=-1`

`(-54)/(x+2)=-1`

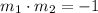
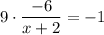
Multiplying both sides by (x+2), we get

`-54=-1(x+2)`

`-54=-x-2`

`-54+2=-x`

`-52=-x`

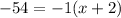
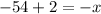
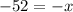
Divide both sides by -1.

`52=x`

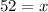
Therefore, the value of x is 52.