Answer:

Explanation:
Hi there!
Vertex form:


Factor out -5 from the first two terms

Complete the square by adding
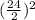 (the square of half of the x-coefficient)
(the square of half of the x-coefficient)
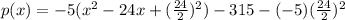
We're subtracting
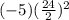 because we need to keep the equation balanced and we can't just add new values.
because we need to keep the equation balanced and we can't just add new values.
Complete the square
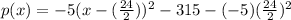
Simplify
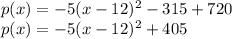
Summary:
- Complete the square
- Simplify
I hope this helps!