Question

Suppose a consumer product researcher wanted to find out whether a highlighter lasted less than the manufacturer's claim that their highlighters could write continuously for 14 hours. The researcher tested 40 highlighters and recorded the number of continuous hours each highlighter wrote before dying. Test the hypothesis that the highlighters wrote for less than 14 continuous hours. X = 13.6 hours, s = 1.3 hours. Report the test statistic, p-value, null hypothesis, conclusion and round to nearest thousandth.

Answer 1

The null hypothesis is
`H_0: \mu = 14`

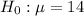
The alternate hypothesis is
`H_a: \mu < 14`

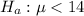
The test statistic is t = -1.95.

The p-value is of 0.0292. This means that for a level of significance of 0.0292 and higher, there is sufficient evidence to conclude that the highlighters wrote for less than 14 continuous hours.

Explanation:

Suppose a consumer product researcher wanted to find out whether a highlighter lasted less than the manufacturer's claim that their highlighters could write continuously for 14 hours.

At the null hypothesis, we test if the mean is 14 hours, that is:

`H_0: \mu = 14`

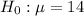
At the alternate hypothesis, we test if the mean is less than 14 hours, that is:

`H_a: \mu < 14`

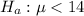
The test statistic is:

`t = (X - \mu)/((s)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis, s is the standard deviation of the sample and n is the size of the sample.

14 is tested at the null hypothesis:

This means that
`\mu = 14`

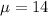
X = 13.6 hours, s = 1.3 hours. Sample of 40:

In addition to the values of X and s given, we have that
`n = 40`

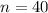
Test statistic:

`t = (X - \mu)/((s)/(√(n)))`

`t = (13.6 - 14)/((1.3)/(√(40)))`

`t = -1.95`

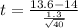
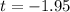
The test statistic is t = -1.95.

P-value:

The p-value of the test is the probability of finding a sample mean lower than 13.6, which is a left tailed test, with t = -1.95 and 40 - 1 = 39 degrees of freedom.

Using a calculator, the p-value is of 0.0292. This means that for a level of significance of 0.0292 and higher, there is sufficient evidence to conclude that the highlighters wrote for less than 14 continuous hours.