Question

A 1200 kg car rounds a curve of radius 80 meters banked at an angle of 20%. What speed must the car travel to experience no friction between the tires and the road?

Answer 1

The speed the car must travel to experience no friction is approximately 16.9 m/s

Step-by-step explanation:

The car and road data are;

The mass of the car, m = 1,200 kg

The radius of the road, r = 80 meters

Given that the angled at which the road is banked, θ = 20°

The friction between the tires and the road, at the required speed,
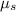`\mu_s` = 0, No friction

We have;

`(v^2)/(r \cdot g) = (\left( sin \, \theta + \mu_s \cdot cos \, \theta \right))/(\left( cos\, \theta + \mu_s \cdot sin\, \theta \right))`

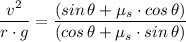
Where
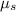`\mu_s` = 0, we get;

`(v^2)/(r \cdot g) = ( sin)/( cos) = tan \, \theta`

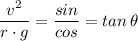
∴ v² = r·g·tan(θ)

Where;

g = The acceleration due to gravity ≈ 9.81 m/s²

v = The speed at which the car travels

∴ v² = 80 m × 9.81 m/s² × tan(20°) = 285.64384 m²/s²

v = √(285.64384 m²/s²) ≈ 16.9 m/s

The speed with which the car must travel to experience no friction, v ≈ 16.9 m/s