Answer:
The speed the car must travel to experience no friction is approximately 16.9 m/s
Step-by-step explanation:
The car and road data are;
The mass of the car, m = 1,200 kg
The radius of the road, r = 80 meters
Given that the angled at which the road is banked, θ = 20°
The friction between the tires and the road, at the required speed,
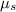 = 0, No friction
= 0, No friction
We have;
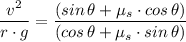
Where
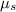 = 0, we get;
= 0, we get;
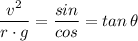
∴ v² = r·g·tan(θ)
Where;
g = The acceleration due to gravity ≈ 9.81 m/s²
v = The speed at which the car travels
∴ v² = 80 m × 9.81 m/s² × tan(20°) = 285.64384 m²/s²
v = √(285.64384 m²/s²) ≈ 16.9 m/s
The speed with which the car must travel to experience no friction, v ≈ 16.9 m/s