Answer:
C
Explanation:
We want to solve the equation:
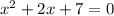
Using the quadratic formula. The quadratic formula is given by:
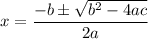
In this case, a = 1, b = 2, and c = 7.
Substitute:
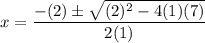
Evaluate:
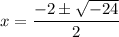
Simplify the square root:
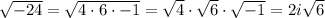
Hence:
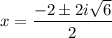
Simplify:
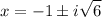
Hence, our solutions are:
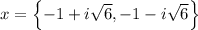
Our answer is C.