Question

A random sample of 40 adults with no children under the age of 18 years results in a mean daily leisure time of 5.65 hours, with a standard deviation of 2.43 hours. A random sample of 40 adults with children under the age of 18 results in a mean daily leisure time of 4.37 hours, with a standard deviation of 1.73 hours. Construct and interpret a 90% confidence interval for the mean difference in leisure time between adults with no children and adults with children. (u1 - u2)

Let u1 represent the mean leisure hours of adults with no children under the age of 18 and u2 represent the mean leisure hours of adults with children under the age of 18. The 90% confidence interval for (u1 - u2) is the range from (???, ???) round to 2 decimals

Answer 1

The 90% confidence interval for (u1 - u2) is the range from; ( 0.50 - 2.06 )

Explanation:

Given the data in the question;

Adult with No children under 18 Adult with children under 18

x"₁ = 5.65 x"₂ = 4.37

s₁ = 2.43 s₂ = 1.73

n₁ = 40 n₂ = 40

with 90% confidence

significance level ∝ = 1 - 90% = 1 - 0.9 = 0.1

Degree of freedom df = 39

Now, since variance are not equal and are also unknown, we will use 2 sample t-distribution method;

Standard Error: σx"₁ - x"₂ =
`\sqrt{(s_1^2)/(n_1) + (s_2^2)/(n_2) }`

Critical value =
`t_{\alpha /2, df` =
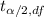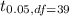`t_{0.05, df=39` = 1.645 { from standard normal table }

Now,

Margin of Error = E =
`t_{\alpha /2, df` ×
`\sqrt{(s_1^2)/(n_1) + (s_2^2)/(n_2) }`

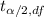we substitute

E = 1.645 ×
`\sqrt{(2.43^2)/(40) + (1.73^2)/(40) }`

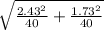
E = 1.645 × √( 0.1476225 + 0.0748225 )

E = 0.7758478

Now, our point difference will be; x"₁ - x"₂ = 5.65 - 4.37 = 1.28

So Limit at 90% confidence interval will be;

x"₁ - x"₂ ± E

Lower Limit = x"₁ - x"₂ - E = 1.28 - 0.7758478 = 0.50415 ≈ 0.50

Upper Limit = x"₁ - x"₂ + E = 1.28 + 0.7758478 = 2.05584 ≈ 2.06

Therefore, The 90% confidence interval for (u1 - u2) is the range from; ( 0.50 - 2.06 )