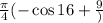Question

Evaluate the given integral by changing to polar coordinates. sin(x2 y2) dAR, where R is the region in the first quadrant between the circles with center the origin and radii 3 and 4

Answer 1

The result of the integral is
`(\pi)/(4)(-cos(16) + \frac{9})`

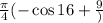
Explanation:

Polar coordinates:

In polar coordinates, we have that:

`x^2 + y^2 = r^2`

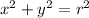
And

`\int \int_(dA) f(x,y) da = \int \int f(r) r dr d\theta`

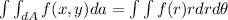
In this question:

`\int \int_(dA) sin((x^2+y^2)) dA = \int \int_(dR) = sin(r^2)r dr d\theta`

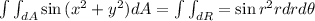
Region in the first quadrant between the circles with center the origin and radii 3 and 4

First quadrant means that
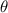`\theta` ranges between
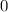`0` and
`(\pi)/(2)`

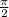
Between these circles means that r ranges between 3 and 4. So

`\int \int_(dR) = sin(r^2)r dr d\theta = \int_(0)^{(\pi)/(2)} \int_(3)^(4) sin(r^2) r dr d\theta`

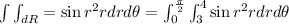
Applying the inner integral:

`\int_(3)^(4) sin(r^2) r dr`

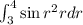
Using substitution, with
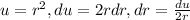`u = r^2, du = 2rdr, dr = (du)/(2r)`, and considering that the integral of the sine is minus cosine, we have:

`-(cos(r^2))/(2)|_(3){4} = (1)/(2)(-cos(16) + \frac{9})`

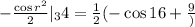
Applying the outer integral:

`\int_(0)^{(\pi)/(2)} (1)/(2)(-cos(16) + \frac{9}) d\theta`

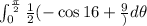
Has no factors of
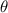`\theta`, so the result is the constant multiplied by
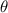`\theta`, and then we apply the fundamental theorem.

`(\theta)/(2)(-cos(16) + \frac{9}) = (\pi)/(4)(-cos(16) + \frac{9})`

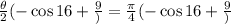
The result of the integral is
`(\pi)/(4)(-cos(16) + \frac{9})`