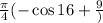Answer:
The result of the integral is
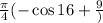
Explanation:
Polar coordinates:
In polar coordinates, we have that:
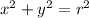
And
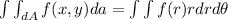
In this question:
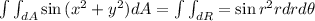
Region in the first quadrant between the circles with center the origin and radii 3 and 4
First quadrant means that
 ranges between
ranges between
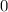 and
and
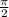
Between these circles means that r ranges between 3 and 4. So
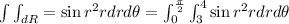
Applying the inner integral:
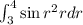
Using substitution, with
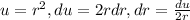 , and considering that the integral of the sine is minus cosine, we have:
, and considering that the integral of the sine is minus cosine, we have:

Applying the outer integral:
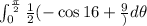
Has no factors of
 , so the result is the constant multiplied by
, so the result is the constant multiplied by
 , and then we apply the fundamental theorem.
, and then we apply the fundamental theorem.

The result of the integral is