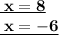- Solve using the quadratic formula ⇨ x² - 2x - 48 = 0.

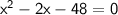
All equations of the form ax² + bx + c = 0 can be solved using the quadratic formula:
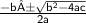 . The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction.
. The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction.
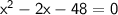
This equation is in standard form: ax² + bx + c = 0 Substitute 1 for a, -2 for b and -48 for c in the quadratic formula.
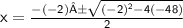
Square -2.
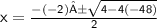
Multiply -4 times -48.
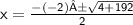
Add 4 to 192.
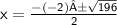
Take the square root of 196.

The opposite of -2 is 2.

Now solve the equation
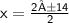 when ± is plus. Add 2 to 14.
when ± is plus. Add 2 to 14.
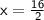
Divide 16 by 2.
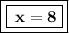
Now solve the equation
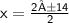 when ± is minus. Subtract 14 from 2.
when ± is minus. Subtract 14 from 2.
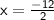
Divide -12 by 2.
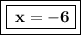
The equation is now solved.