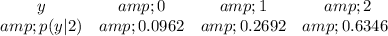Answer:
(a)
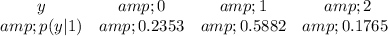
(b)
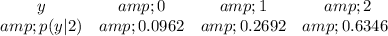
Explanation:
Given

Solving (a): Find PMF of y if x = 1
This implies that, we consider the dataset of the row where x = 1 i.e.

The PMF of y given x is calculated using:
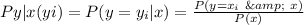
When x = 1
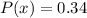 --- the sum of the rows
--- the sum of the rows
So, we have:
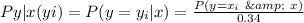
For i = 0 to 2, we have:

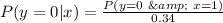
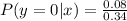


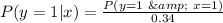
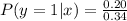
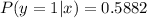


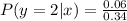
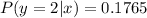
So, the PMF of y given that x = 1 is:
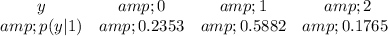
Solving (b): The interpretation of (b) is to find the PMF of y if x = 2
This implies that, we consider the dataset of the row where x = 2 i.e.

When
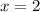
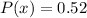
So, we have:
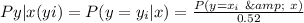
For i = 0 to 2, we have:

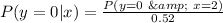
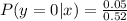


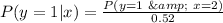
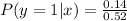
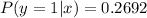


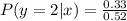
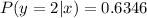

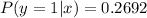
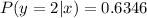
So, the PMF of y given that x = 1 is: