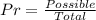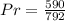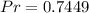Question

Carlos has chosen 12 different CDs he would like to buy: 4 are rap music, 5 are country, and 3 are heavy metal. He has only enough money to buy 5 of them (each CD costs the same price). So he selects 5 of them at random. What is the probability that his purchase includes at least one CD from each of the three genres.

Answer 1

The probability is 0.7449

Explanation:

Given

`n = 12` ---- total

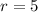`r = 5` --- selection

`Genre =\{Rap(4), Country (5), Heavy\ metal (3)\}`

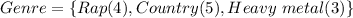
Required

Probability of buying at least 1 of each genre

First, we calculate the total possible selection.

To select 5 CDs from a total of 12, we use:

`^nC_r = (n!)/((n - r)!r!)`

`^(12)C_5 = (12!)/((12 - 5)!5!)`

`^(12)C_5 = (12!)/(7!5!)`

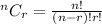
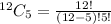
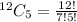
Expand

`^(12)C_5 = (12*11*10*9*8*7!)/(7!*5*4*3*2*1)`

`^(12)C_5 = (12*11*10*9*8)/(5*4*3*2*1)`

`^(12)C_5 = (95040)/(120)`

`^(12)C_5 = 792`

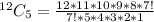
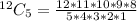
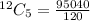
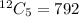
So, the total selection is:

`Total = 792`

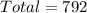
To select at least 1 from each genre, there are 6 possible scenarios.

And they are:

`\begin{array}{ccc}{Heavy\ Metal (3)} & {Rap (4)} & {Country(5)} & {3} & {1} & {1} & 2 & {1} & {2} & {2} & {2} & {1}& {1} & {2} & {2}& {1} & {3} & {1}& {1} & {1} & {3} \ \end{array}`

The possible selections for the given scenario is:

`Possible = ^3C_3* ^4C_1 * ^5C_1 +^3C_2* ^4C_1 * ^5C_2 +^3C_2* ^4C_2 * ^5C_1 +^3C_1* ^4C_2 * ^5C_2 +^3C_1* ^4C_3 * ^5C_1 +^3C_1* ^4C_1 * ^5C_3`

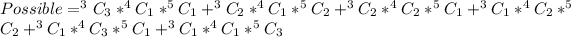
Using a calculator, we have:

`Possible = 1*4*5 +3*4*10 +3*6*5 +3*6*10+3*4*5+3*4*10`

`Possible= 20 +120 +90 +180+60+120`

`Possible = 590`

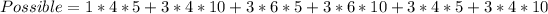
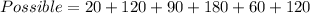
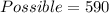
The probability is then calculated using:

`Pr = (Possible)/(Total)`

`Pr = (590)/(792)`

`Pr = 0.7449`