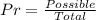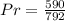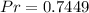Answer:
The probability is 0.7449
Explanation:
Given
 ---- total
---- total
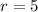 --- selection
--- selection
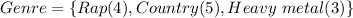
Required
Probability of buying at least 1 of each genre
First, we calculate the total possible selection.
To select 5 CDs from a total of 12, we use:
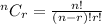
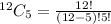
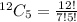
Expand
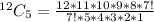


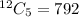
So, the total selection is:
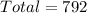
To select at least 1 from each genre, there are 6 possible scenarios.
And they are:

The possible selections for the given scenario is:
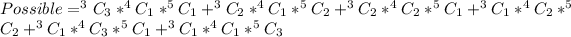
Using a calculator, we have:
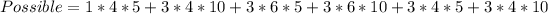

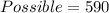
The probability is then calculated using: