This question is incomplete, the missing image is uploaded along this answer below.
Answer:
the speed of the 50-kg cylinder after it has descended is 3.67 m/s
Step-by-step explanation:
Given the data in the question and the image below;
relation between velocity of cylinder and velocity of the drum is;
V
 = ω
= ω
 × r
× r
 ----- let this be equ 1
----- let this be equ 1
where V
 is velocity of cylinder, ω
is velocity of cylinder, ω
 is the angular velocity of drum C and r
is the angular velocity of drum C and r
 is the radius of drum C
is the radius of drum C
Now, Angular velocity of gear B is;
ω
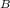 = ω
= ω

ω
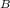 = V
= V
 / r
/ r
 -------- let this equ 2
-------- let this equ 2
so;
V
 / 0.1 m = 10V
/ 0.1 m = 10V

Next, we determine the angular velocity of gear A;
from the diagram;
ω
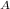 ( 0.15 m ) = ω
( 0.15 m ) = ω
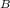 ( 0.2 m )
( 0.2 m )
from equation 2; ω
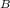 = V
= V
 / r
/ r

so
ω
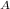 ( 0.15 m ) = (V
( 0.15 m ) = (V
 / r
/ r
 ) 0.2 m
) 0.2 m
substitutive in value of radius r
 (0.1 m)
(0.1 m)
ω
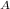 ( 0.15 m ) = (V
( 0.15 m ) = (V
 / 0.1 m ) 0.2 m
/ 0.1 m ) 0.2 m
ω
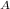 ( 0.15 ) = 0.2V
( 0.15 ) = 0.2V
 / 0.1
/ 0.1
ω
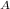 = 2V
= 2V
 / 0.15
/ 0.15
ω
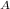 = 13.333V
= 13.333V
 ----- let this be equation 3
----- let this be equation 3
To get the speed of the cylinder, we use energy conversation;
assuming that the final position is;
T₁ + ∑
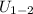 = T₂
= T₂
0 + m
 gh =
gh =
 m
m
 V²
V²
 +
+
 ω²
ω²
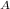 +
+
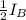 ω²
ω²
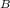
so
m
 gh =
gh =
 m
m
 V²
V²
 +
+
 (m
(m
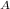 k
k
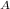 ²)(13.333V
²)(13.333V
 )² +
)² +
 (m
(m
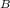 k
k
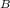 ²)(10V
²)(10V
 )²
)²
we given that; m
 = 50 kg, h = 2 m, m
= 50 kg, h = 2 m, m
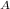 = 10 kg, k
= 10 kg, k
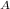 125 mm = 0.125 m, m
125 mm = 0.125 m, m
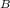 = 30 kg, k
= 30 kg, k
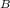 = 150 mm = 0.15 m.
= 150 mm = 0.15 m.
we know that; g = 9.81 m/s²
so we substitute
50 × 9.81 × 2 = (
 × 50 × V
× 50 × V
 ²) +
²) +
 ( 10 × (0.125)² )(13.333V
( 10 × (0.125)² )(13.333V
 )² +
)² +
 ( 30 × (0.15)²)(10V
( 30 × (0.15)²)(10V
 )²
)²
981 = 25V
 ² + 13.888V
² + 13.888V
 ² + 33.75V
² + 33.75V
 ²
²
981 = 72.638V
 ²
²
V
 ² = 981 / 72.638
² = 981 / 72.638
V
 ² = 13.5053
² = 13.5053
V
 = √13.5053
= √13.5053
V
 = 3.674955 ≈ 3.67 m/s
= 3.674955 ≈ 3.67 m/s
Therefore, the speed of the 50-kg cylinder after it has descended is 3.67 m/s