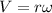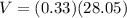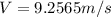Question

A student decides to give his bicycle a tune up. He flips it upside down (so there's no friction with the ground) and applies a force of 34 N over 0.6 seconds to the pedal, which has a length of 16.5 cm. If the back wheel has a radius of 33.0 cm and moment of inertia of 1200 kg cm^2, what is the tangential velocity of the rim of the back wheel in m/s

Answer 1

`V=9.2565m/s`

Step-by-step explanation:

From the question we are told that:

Force
`F = 34 N`

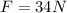
Time
`t = 0.6 s`

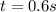
Length of pedal
`l_p=16.5cm \approx0.165m`

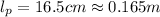
Radius of wheel
`r = 33 cm = 0.33 m`

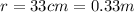
Moment of inertia,
`I = 1200 kgcm2 = 0.12 kg.m2`

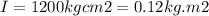
Generally the equation for Torque on pedal
`\mu` is mathematically given by

`\mu=F*L\\\mu=34*0.165`

`\mu=5.61N.m`

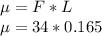
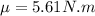
Generally the equation for angular acceleration
`\alpha` is mathematically given by

`\alpha=(\mu)/(l)`

`\alpha=(5.61)/(0.12)`

`\alpha=46.75`

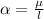
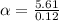
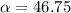
Therefore Angular speed is \omega

`\omega=\alpha*t`

`\omega=(46.75)*(0.6)`

`\omega=28.05rad/s`

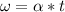
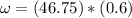
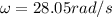
Generally the equation for Tangential velocity V is mathematically given by

`V=r\omega`

`V=(0.33)(28.05)`

`V=9.2565m/s`