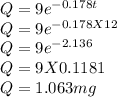Answer:
a. dQ/dt = -kQ
b.
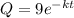
c. k = 0.178
d. Q = 1.063 mg
Explanation:
a) Write a differential equation for the quantity Q of hydrocodone bitartrate in the body at time t, in hours, since the drug was fully absorbed.
Let Q be the quantity of drug left in the body.
Since the rate of decrease of the quantity of drug -dQ/dt is directly proportional to the quantity of drug left, Q then
-dQ/dt ∝ Q
-dQ/dt = kQ
dQ/dt = -kQ
This is the required differential equation.
b) Solve your differential equation, assuming that at the patient has just absorbed the full 9 mg dose of the drug.
with t = 0, Q(0) = 9 mg
dQ/dt = -kQ
separating the variables, we have
dQ/Q = -kdt
Integrating we have
∫dQ/Q = ∫-kdt
㏑Q = -kt + c
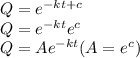
when t = 0, Q = 9

So,
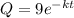
c) Use the half-life to find the constant of proportionality k.
At half-life, Q = 9/2 = 4.5 mg and t = 3.9 hours
So,
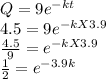
taking natural logarithm of both sides, we have

d) How much of the 9 mg dose is still in the body after 12 hours?
Since k = 0.178,
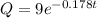
when t = 12 hours,