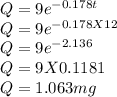Question

Hydrocodone bitartrate is used as a cough suppressant. After the drug is fully absorbed, the quantity of drug in the body decreases at a rate proportional to the amount left in the body, with constant of proportionality k. Suppose that the half-life of hydrocodone bitartrate in the body is 3.9 hours, and that the oral dose taken is 9 mg.

a) Write a differential equation for the quantity Q of hydrocodone bitartrate in the body at time t, in hours, since the drug was fully absorbed.
b) Solve your differential equation, assuming that at the patient has just absorbed the full 9 mg dose of the drug.
c) Use the half-life to find the constant of proportionality k.
d) How much of the 9 mg dose is still in the body after 12 hours?

Answer 1

a. dQ/dt = -kQ

b.
`Q = 9e^(-kt)`

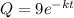
c. k = 0.178

d. Q = 1.063 mg

Explanation:

a) Write a differential equation for the quantity Q of hydrocodone bitartrate in the body at time t, in hours, since the drug was fully absorbed.

Let Q be the quantity of drug left in the body.

Since the rate of decrease of the quantity of drug -dQ/dt is directly proportional to the quantity of drug left, Q then

-dQ/dt ∝ Q

-dQ/dt = kQ

dQ/dt = -kQ

This is the required differential equation.

b) Solve your differential equation, assuming that at the patient has just absorbed the full 9 mg dose of the drug.

with t = 0, Q(0) = 9 mg

dQ/dt = -kQ

separating the variables, we have

dQ/Q = -kdt

Integrating we have

∫dQ/Q = ∫-kdt

㏑Q = -kt + c

`Q = e^(-kt + c)\\Q = e^(-kt)e^(c)\\Q = Ae^(-kt) (A = e^(c))`

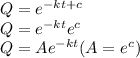
when t = 0, Q = 9

`Q = Ae^(-kt) \\9 = Ae^(-k0)\\9 = Ae^(0)\\9 = A\\A = 9`

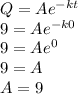
So,
`Q = 9e^(-kt)`

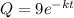
c) Use the half-life to find the constant of proportionality k.

At half-life, Q = 9/2 = 4.5 mg and t = 3.9 hours

So,

`Q = 9e^(-kt)\\4.5 = 9e^(-kX3.9)\\(4.5)/(9) = e^(-kX3.9)\\(1)/(2) = e^(-3.9k)\\`

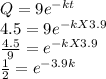
taking natural logarithm of both sides, we have

`ln(1)/(2) = ln(e^(-3.9k))\\\\-ln2 = -3.9k\\k = -ln2/-3,9 \\k = -0.693/-3.9\\k = 0.178`

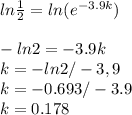
d) How much of the 9 mg dose is still in the body after 12 hours?

Since k = 0.178,

`Q = 9e^(-0.178t)`

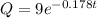
when t = 12 hours,

`Q = 9e^(-0.178t)\\Q = 9e^(-0.178X12)\\Q = 9e^(-2.136)\\Q = 9 X 0.1181\\Q = 1.063 mg`