Given:
Dimensions of a block are
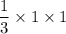 .
.
To find:
The number of block that can be fit in a unit cube.
Solution:
Volume of a cuboid is:

Where, l is length, b is breadth or width and h is the height of the cuboid.
So, the volume of the given block is:
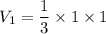
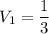
Dimensions of a unit cube are
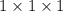 . So, the volume of the unit cube is:
. So, the volume of the unit cube is:
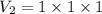
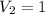
We need to divide the volume of unit cube by the volume of a block to find the number of block that can be fit in a unit cube.
So, the number of blocks that fit in a unit cube is:

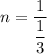
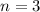
Therefore, the correct option is B.