Answer:
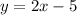 , see below.
, see below.
Explanation:
There is enough information to make a point slope equation that we can later convert into slope intercept.
Point slope form is:
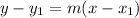
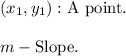
We are given the slope of 2 and the point (4,3).
Replace the variables with the given information.

With the equation we will now convert it into slope intercept form:
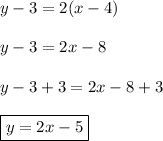
Hope this helps!