Question

Please Help!

Your family's new business is finally starting to get on track. You started with an investment of $20,000, but lost 10% the first year, 6% the second year, and 3$ the third year. During the fourth year, however, you gained 5%

(A) How much money did you have after the first three years?

(B) What was the cumulative decay factor after the first three years?

(C) What was the cumulative factor after the first four years? Does this factor represent decay or growth?

(D) What percent increase do you need to get during the fifth year to break even (end up with $20,000)?​

Answer 1

A)

$16412.40.

B)

Our culminate decay factor was 0.82062.

C)

0.861651. It represents decay because it's less than one.

D)

We need at least a 16.1% increase.

Explanation:

We started off with $20,000. In the first year, we lost 10%. In the second year, we lost an additional 6%, and another 3% in the third year. During the fourth year, however, we regained 5%.

Part A)

In the first year, we lost 10% of our original investment. In other words, we will have left 100% - 10% or 90% of our original investment. So, after the first year, we will have:

`20000(0.9)=\$ 18000`

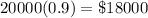
During the second year, we lost another 6%. So, it will be 100% - 6% = 94% = 0.94 of our current investment. So, after the second year, we will have:

`18000(0.94)=\$ 16920`

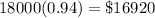
Finally, during the third year, we lost 3%. So, it will be 100% - 3% = 0.97 of our current investment:

`16920(0.97)=\$ 16412.4`

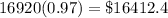
After the first three years, our investment dwindled down to $16412.40.

Part B)

We started off with $20,000 and ended up with $16412.40. Let r represent the decay factor. We can write the following equation:

`20000d=16412.4`

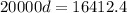
This reads, "our original investment of $20,000 by multiplied by some (decay) factor equals our current investment of $16412.4."

Solve for d:

`\displaystyle d=(16412.4)/(20000)=0.82062`

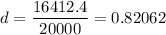
So, our decay factor is 0.82062.

(Note: This means that our rate of decay was 1 - 0.82062 = 0.17938. So, we lost approximately 18% of our investment over the course of the three years.)

Part C)

After the third year, our investment was $16412.40.

During the fourth year, we gained 5% on our investment. So, it will be 100% + 5% = 105% = 1.05 of our current investment:

`16412.4(1.05)=\$ 17233.02`

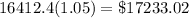
Again, we can write an equation:

`20000d=17233.02`

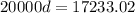
Where d represents the culminative factor after four years.

Solving for d yields:

`d=0.861651`

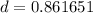
Since the culminative factor is less than one, this is decay.

Decay is also correct contextually, since after four years, our current investment is lower than our original investment.

Part D)

After the fourth year, we have $17233.02.

In order to find the percent increase to rereach $20,000, we can write an equation:

`17233.02d=20000`

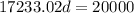
Solving for d yields:

`\displaystyle d\approx 1.1606`

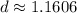
So, the growth factor is about 1.1606.

This means that during the fifth year, we will need to grow by 1 - 1.1606 or about 16.1% in order to rereach our original investment of $20,000.